Next: Analysis of experiments Up: Longitudinal electrodynamic forces Previous: Experiments
![]()
![]()
![]()
![]()
Next: Analysis
of experiments Up: Longitudinal
electrodynamic forces Previous: Experiments
As we have seen, longitudinal forces can be a quite fruitful idea to understand some experiments. In this chapter we shall study the various theoretical approaches that have been made. A new investigation, based on Maxwell stresses, is given and is compared with the others.
Graneau has proposed the use of Ampère electrodynamics, based on Ampère's original formula, to account for the longitudinal stress. With the aid of a numerical method, finite current element analysis, he has estimated the stress predicted by Ampère's formula.
We begin with studying the way longitudinal stress actually arises from Ampère's formula and the problems with its computation. Maxwell stresses could also account for longitudinal stress. This is analyzed and compared with the Ampère electrodynamics. The relation between the approaches and the possibility of deriving Ampère's formula from classical electrodynamics is then discussed.
Relativistic electric fields and electric fields from surface charges have been advocated to predict longitudinal stress. This is analysed in the last sections, where the Ampère formula and other 2:nd order relativistic theories are put into context. The conclusions drawn from the discussion are summed up, ending the chapter.
During the last debate, the main theory to account for longitudinal stress has been the Ampère electrodynamics, revived by Graneau. It is based on Ampère's original formula:
![]()
Here ![]() is the force current element 1 (
is the force current element 1 ( ![]() ) exerts on current element 2 (
) exerts on current element 2 ( ![]() );
); ![]() and
and ![]() are the electric currents in the circuits;
are the electric currents in the circuits; ![]() is the magnetic permeability;
is the magnetic permeability; ![]() and
and ![]() are vectors in the direction of a current element, see Figure 3.1A;
are vectors in the direction of a current element, see Figure 3.1A;
![]() is the distance between the current elements; and
is the distance between the current elements; and ![]() the unit vector from
the unit vector from ![]() to
to ![]() .
.
When deducing his formula, Ampère assumed that it would obey Newton's third law -- i.e. that the forces between the current elements would be equal and opposite, and directed in the line between them. Ampère considered this a natural mathematical assumption, and it could neither be proved nor disproved from experiments with the interaction between closed circuits.
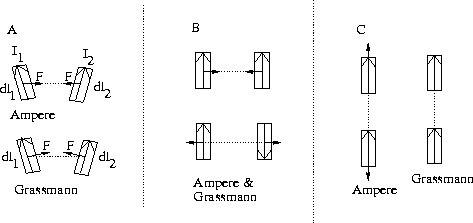
Figure 3.1: The forces between two current elements according to
Ampère's and Grassmann's equations. (A) Forces between current
elements.
(B) Transverse forces between parallel elements. (C) Longitudinal
forces
between co-linear elements
As with the Grassmann law,
![]()
two parallel current elements attract, and two anti-parallel repel, Figure 3.1B. But for co-linear elements the Ampère formula differs and predicts a repulsion, whereas the Grassmann force is zero, Figure 3.1C. (This was actually the criterion Grassmann used to derive his formula, as he thought the Ampère force behaved strangely.)
A long thin conductor would then experience a tension along itself, according to Ampère's formula. As we have seen, this was the argument used by Ampère to propose the hairpin experiment.
Actually, if the conductor is viewed as a bunch of filaments, current elements beside each other should attract, whereas they would repel their colinear neighbours, Figure 3.2A. The situation resembles very much stacking magnets side by side in a rectangular pipe, Figure 3.2B. The `like' poles repel each other in the longitudinal direction (along the `conductor'). The unlike poles in the transverse direction attract. As a result the `conductor' experiences a longitudinal repulsion that is diluted, and a transverse pinch, just like a real conductor.
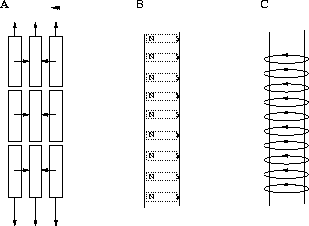
Figure 3.2: The `stacked magnets' analogy. (A) Forces inside a
conductor
according to Ampère's force law. (B) Stacked magnets. (C)
Magnetic
flux around a current.
Imagining the magnets as circular, or circular flux, one understands why the analogy is good. (By folding each magnet into a circular flux loop, we get something that looks very much like the magnetic field associated with the current in a conductor, Figure 3.2C.)
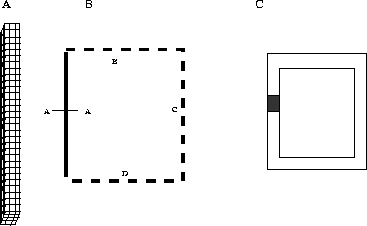
Figure 3.3: (A) Subdivision of a straight conductor. (B) Omitted
parts. (C) Small segment of a circuit.
When trying to estimate the longitudinal stress, one runs into difficulties, as singularities arise when integrating the circuit around itself. This is due to the line current formulation. In order to avoid this Graneau has devised a method: `Finite current element analysis'. The circuit is subdivided into filaments, Figure 3.3A, and integrated numerically. Subsequent iterations converge quite rapidly, as the repulsive force is `diluted' by the side-by-side attraction.
Graneau has estimated the stress of a long straight conductor by calculating the forces all the current elements in the upper part exert on those in the lower part. This would give the stress across the middle section, A-A in Figure 3.3B.
The method is not unambiguous however. One question is if the stress is uniform or non-uniform, as the above approach mixes the two kinds of stresses.
Let us first consider non-uniform stress. This would arise if there were a difference in longitudinal force between two adjacent current elements; the difference would then be interpreted as stress, Figure 3.4A. One problem with the above method is the omission of parts of the circuit, the dotted lines in Figure 3.3B . The reason the other sides cannot be neglected is that a current element only experiences the sum of the forces from the rest of the circuit, as the element is not aware of from where the forces come.
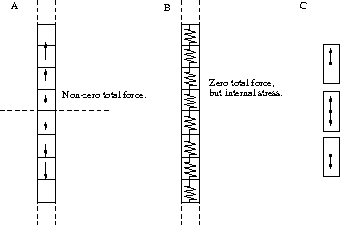
Figure 3.4: (A) Non-uniform stress. (B) Uniform stress. (C)
Cancellation
of forces.
How much is then neglected? The force on a short segment of a conductor, exerted by the rest of the circuit, was calculated. The longitudinal part of the force turned out to approach zero as the subdivision was made finer. Actually this is not as surprising as it seems. Only a non-uniform stress would reveal itself with this kind of analysis.
The stress is obviously more uniform in character. (The net force on an individual current element is zero in the axial direction, but the conductor is in a state of stress, as visualized by a series of strained springs in Figure 3.4B.) To predict such a stress the force between two adjacent current elements is essential. But these forces cancel out when forces from both sides of a current element are considered, as they are equal and opposite, Figure 3.4C. Thus the above reasoning does not give any clues into how to perform a calculation of the stress unambiguously. As we shall see though, there exist methods to estimate the stress.
During the debate in the 80s it has been tacitly assumed that longitudinal forces and stress cannot be predicted from classical electrodynamics. The arguments have been based on the fact that the Lorentz equation only predicts a transverse magnetic force. By focusing on the field properties rather than the charge carriers, I intend to show that Maxwell stresses, and thus classical electrodynamics, indeed can be interpreted to predict longitudinal stress.
The magnetic part of the Maxwell stress (the one of relevance in this discussion) is:
![]()
Here ![]() and
and ![]() are the magnetic induction and field, respectively; and
are the magnetic induction and field, respectively; and ![]() is the outward directed surface element. When integrating the
expression
around a body it yields the total force on it. For a moving charge we
recover
the Lorentz force. Forces on opposite surfaces that cancel under
integration
are also of interest as these predict stress in the body, this approach
can e.g. be used to calculate the pinch pressure. As we shall see, the
longitudinal forces reveal themselves in a similar way.
is the outward directed surface element. When integrating the
expression
around a body it yields the total force on it. For a moving charge we
recover
the Lorentz force. Forces on opposite surfaces that cancel under
integration
are also of interest as these predict stress in the body, this approach
can e.g. be used to calculate the pinch pressure. As we shall see, the
longitudinal forces reveal themselves in a similar way.
If we investigate the above expression we find that there exists a tension along the lines of flux, tending to shorten them, and a pressure between them, making them repel each other. Magnetic attraction and repulsion is easily visualized, Figure 3.5.
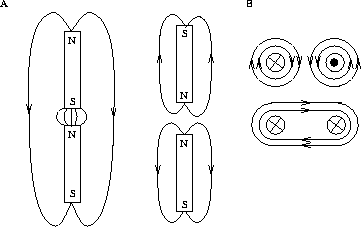
Figure 3.5: Attraction and repulsion between magnets as a result
of Maxwell stresses: (A) Magnets. (B) Currents.
Consider a straight conductor segment. In a straight conductor the magnitude of the forces only depends on the radial distance, whereas their direction depend on the orientation of the bounding surface. The Maxwell stress tends to split the conductor in the axial direction, the stress being strongest near the periphery, Figure 3.6A. In the tangential direction (along the flux lines) there is a tension. Thus two pieces of a axially split conductor attract each other, Figure 3.6B. In the radial direction a contraction exists which causes the pinch pressure, Figure 3.6C.
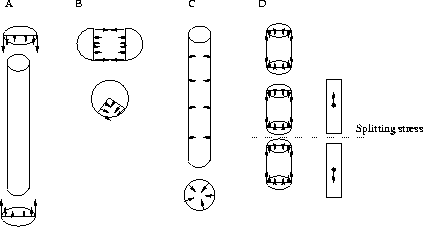
Figure 3.6: Maxwell stresses across different surfaces. (A)
Axial
stress, (B) Tangential stress, (C) Radial stress, (D) Splitting axial
stress
compared with repelling current elements.
From Figure 3.6D it is easy to see the similarity to the tension predicted by {Ampère's equation. With a uniform current density (J) in the conductor we get:
![]()
for the magnetic field H at distance r from the
center.
R is the radius of the conductor. The magnitude of the stress ![]() is:
is:
![]()
where we have introduced I as the total current.
Integrated across the axial surface we have,
![]()
or
![]()
for the mean splitting stress and the splitting force, respectively.
In this way one could imagine how this force could cause the initial
separation in the multiarc generator, and how the combined effect of
the
radial shear and the axial tension could break the wire in Nasi ![]() owski's experiment.
owski's experiment.
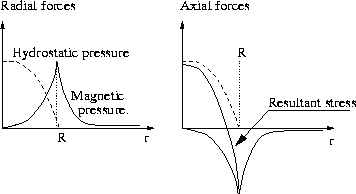
Figure 3.7: Radial and axial stresses in a liquid conductor.
Let us now examine a cylindric liquid conductor, as in Figure 3.6 (Regard the previous solid conductor as liquid). The radial magnetic pressure sets up stress in the conductor. This stress is balanced by the resulting hydrostatic pressure, when the system is at equilibrium. In the axial surface forces tending to compress the segment are set up. This compressive stress is greatest at the periphery and zero in the middle. The hydrostatic pressure, on the other hand, is zero at the periphery and has its maximum at the center. Thus these forces do not balance in the axial direction, Figure 3.7. (This transfer of radial pressure into axial is not present in solid conductors.) At the center the hydrostatic pressure dominates, causing the conductor to stretch itself there. At the periphery, where the magnetic pressure dominates, the conductor tends to contract.
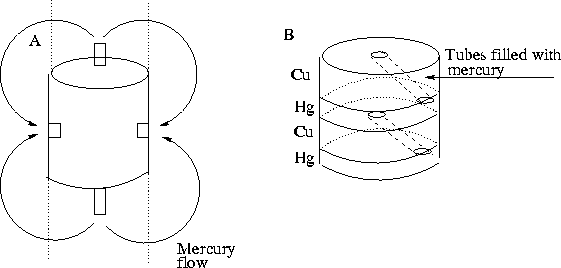
Figure 3.8: (A) Experiment to demonstrate the stretching in the
middle. (B) Device to enhance the pressure.
This gives some insight into how the pinch pressure works. As the hydrostatical pressure is stronger than the axial Maxwell stress at the center, the conductor expands axially (if it has freedom to do so), at its center. Northrup devised an experiment to demonstrate the stretching in the middle, Figure 3.8A. The electric current flows in the axial direction. Due to the resulting pressures, mercury flows out from the center and recirculates back at the periphery. The pressure can be enhanced by adding it `in series', as in Northrup's second experiment, Figure 3.8B. The pressure at the center of one mercury segment is connected to the periphery of the next one, et cetera. The pressure can be used to monitor the current with the aid of a manometer.
Various attempts have been made to prove the equivalence or non-equivalence of the Lorenz-Grassmann force law and the Ampère force law. We are not going to digress into this discussion here. Most of the arguments have been about proving that no net longitudinal force exists on a part of a conductor. The main problem with these reasonings is that they cannot reveal a uniform stress -- whether it exists or not in the law under consideration.
A more interesting question is the possibility of deriving Ampère's law from field theory. Rambaut [57] has derived Weber's electrodynamical potential from the relativistic potentials. From the Weber potential it is then straightforward to derive Ampère's formula. Assis [3] has shown that this is possible even with the modern idea of a current element (moving electrons and stationary ions) [3]. Other derivations of Ampère's law from relativistic potentials are also possible [56]. However, it is important to note that Neumann's force law (and potential) is a special case, applying only to interactions between closed circuits. It can be derived both from Ampère's and Grassmann's laws, and thus cannot be used to discriminate between the two, nor to prove their equivalence, although this is sometimes claimed.
The question arises whether it is necessary to use relativistic potentials to derive Ampère's force law. Could a relation be brought between Ampère's formula and the magnetic Maxwell stresses?
In order to understand the problem, let us consider the analogous case of a long charged rod. For a rod with radius R we have,
![]()
where ![]() is the electric field;
is the electric field; ![]() the volume charge density;
the volume charge density; ![]() is the electric permittivity of vacuum; and
is the electric permittivity of vacuum; and ![]() is the unit vector in the radial direction. As above, r is the
radial
distance from the center.
is the unit vector in the radial direction. As above, r is the
radial
distance from the center.
An electrical Maxwell stress will act, tending to stretch the rod. With,
![]()
for the force on a circular cross-section, we have:
![]()
Here ![]() is the unit normal to the circular surface, directed outwards from a
volume
element.
is the unit normal to the circular surface, directed outwards from a
volume
element.
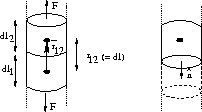
Figure 3.9: Adjacent elements in the rod.
If we now regard this separating force as being the repulsion between two adjacent volume elements, we should arrive with something that looks like the Coulomb law, with some geometrical correction factor. Hence:
![]()
(Note that ![]() means the distance between two current elements, and should not be
confused
with r.) Thus the view of Maxwell stress across the surface,
and
the view of line-charges repelling each other show a close
relationship.
means the distance between two current elements, and should not be
confused
with r.) Thus the view of Maxwell stress across the surface,
and
the view of line-charges repelling each other show a close
relationship.
Now substitute the rod by a long conductor. The magnetic field from the current is:
![]()
Here I is the electric current and ![]() is the unit vector in the tangential direction. The Maxwell stress on
the
circular surface is:
is the unit vector in the tangential direction. The Maxwell stress on
the
circular surface is:
![]()
![]()
where the left part of the expression is recognized as the Ampère force between two colinear current elements. As mentioned before, Ampère had to assume that the force was in the line in between the current elements (and thus obeying Newton's third law), as he couldn't derive it from experiment. Let us now assume that the force between adjacent colinear current elements actually is
![]()
This is quite reasonable as we in the electrostatical case have the Coulomb force in the corresponding expression. Could this be used to uniquely define a force law, e.g. Ampère's? As we shall see, the answer is quite in the affirmative.
Analysing Ampère's experiments, without the assumption of Newton's third law, Whittaker [67] derived the following expression for the most general force law:
![]()
A and B are here numerical constants that cannot be evaluated from Ampère's own experiments. However, from the reasoning about the Maxwell stress above we arrived with
![]()
for the force between adjacent co-linear current elements. This is equivalent to having
![]()
or
![]()
We thus have a formula that is symmetric in ![]() and
and ![]() . Whittaker arrived with the same result from considerations of linear
force balance (from aestethic rather than experimental considerations).
. Whittaker arrived with the same result from considerations of linear
force balance (from aestethic rather than experimental considerations).
Is there any way we could determine the remaining constant? Aspden [1] noted another condition that can be put on the force law, by analysing an experiment performed by Trouton and Noble [66]. (They found that a capacitor showed no tendency to turn when in linear motion transverse to its suspension.) Aspden concludes:
`There is no interaction torque out of balance between anti-parallel current elements ...To satisfy [this] observation, terms other than those in
must cancel when
is equal to
.'
This means that A = B and, as we already have A= -B, we get A=B=0, or Ampère's force law:
![]()
(Strictly speaking, one may question whether the current elements in metallic conduction currents, and those in a capacitor moving sideways can be considered equivalent, as Aspden's reasoning implies. It is a remarkable fact though, that when so is done, one arrives with Ampère's formula. Anyway, the value of the second constant doesn't affect the repulsion between co-linear current elements.)
Thus we more or less experimentally (as the Maxwell stress can
explain
the longitudinal forces) have derived Ampère's formula, without
the additional assumption of the law obeying Newton's third law. Of
course,
taking the route over field theory doesn't make the derivation as clear
cut as Ampère's. In a sense we have shown that Ampère's
formula
can be inferred from field theory![]() .
The above reasoning is not intended to be any rigorous proof, but
rather
to show the intuitive value of both the views.
.
The above reasoning is not intended to be any rigorous proof, but
rather
to show the intuitive value of both the views.
But from the reasoning it is clear that Graneau's finite current element analysis overestimates the tension, even if just the interaction between two filamentary current elements is considered. (The stress predicted should be the same as the mean Maxwell stress, but Graneau reports a stress about ten times greater, from his calculations.) The same problems arise when trying to calculate electric stresses with Coulomb's law.
We can see how Ampère's law, when it comes to forces in a conductor, plays the same part as Coulomb's law does in electrostatics. Maxwell stresses and Ampère's formula turn out to be two complementary views -- one focuses on the field properties and the other on current elements -- Maxwell stresses being the simplest to use in my view.
In what respects does Ampère electrodynamics then differ from field theory? When it comes to longitudinal forces they are obviously saying quite the same thing. But is there anything else in the Ampère electrodynamics that is interesting and not apparent in classical electrodynamics?
From Ampère's law several action at a distance theories have been derived [45]. The most general of these is the one derived by Moon and Spencer [46]. It is a 2:nd order theory, i.e. it includes 2:nd order relativistic effects, such as the relativistic electric field. Several paradoxes in electromagnetic induction (dealing with e.g. homopolar and moving boundary induction) are easily solved within this theory [48, 49]. Thus being on the threshold between classical and relativistic electrodynamics, it may be useful for calculations.
Another 2:nd order theory is the Darwin formulation, which is easily derived from the relativistic potentials [39]. It has shown to be useful in plasma physics calculations [41], though it does not, as the Moon and Spencer formulation, include radiation effects.
An overview of the different theories is given below:
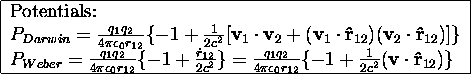
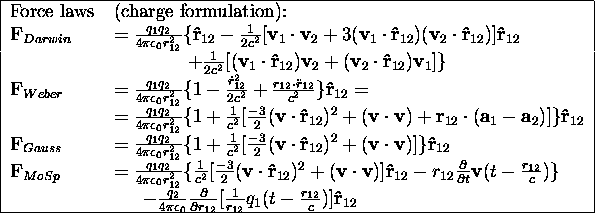
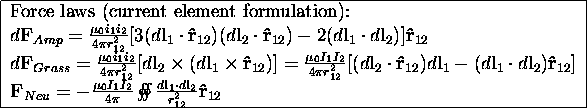
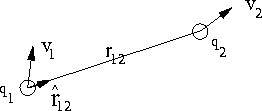
Figure 3.10: The meaning of the different vectors.
Here ![]() is the force charge 1 (
is the force charge 1 ( ![]() ) exerts on charge 2 (
) exerts on charge 2 ( ![]() );
); ![]() and
and ![]() are the velocities of the charges;
are the velocities of the charges; ![]() their relative velocity;
their relative velocity; ![]() and
and ![]() are their accelerations;
are their accelerations; ![]() is the vector from charge 1 (
is the vector from charge 1 ( ![]() ) to charge 2 (
) to charge 2 ( ![]() );
); ![]() is its first derivative, or the relative velocity projected on the line
between the charges; and
is its first derivative, or the relative velocity projected on the line
between the charges; and ![]() the second derivative, which can be expanded into and expression of the
velocities and accelerations.
the second derivative, which can be expanded into and expression of the
velocities and accelerations.
As can be seen, Gauss' and Weber's laws differ only in the acceleration terms. Consequently they are equivalent in magnetostatics. As Gauss formula doesn't contain any acceleration terms, it alone cannot predict electromagnetic induction, whereas Weber's law can.
Figure 3.11: Relationships of the force laws.
Ivezic suggested that relativistic electric fields could account for longitudinal forces. What then, is the relativistic electric field? In classical electrodynamics it is assumed that a conductor with an equal number of positive a negative charges (neutral) is experienced as charge neutral, even though the electrons are moving. Relativistically it cannot be so.
Consider a long straight conductor that is charge neutral, and then
switch on a current. We still have the same number of electrons. But as
they are moving, the spacing between them shrink (the Lorentz
contraction)
and we observe a charge density from them that is higher than when at
rest.
Let the charge density for positive and negative charge at rest be: ![]() and
and ![]() respectively. Then, when the electrons are moving we observe, in the
laboratory
frame, a charge density from them that is
respectively. Then, when the electrons are moving we observe, in the
laboratory
frame, a charge density from them that is ![]() . For the total observed charge we have:
. For the total observed charge we have:
![]()
where v is the drift velocity of the electrons, and

Hence the conductor behave as if it had an excess negative charge,
and
is surrounded by an `electric' field, the relativistic (or 2:nd order)
electric field. Normally this field is much weaker than the magnetic
field.
Between two metallic `neutral' conductors the resultant force will be
proportional
to ![]() , as the field is produced by the
, as the field is produced by the ![]() fraction in one of the conductors, and experienced only by a similar
fraction
in the other conductor.
fraction in one of the conductors, and experienced only by a similar
fraction
in the other conductor.
However, when it comes to forces on the charges within one and the same conductor, the situation is quite different. Then the relativistic electric field is of the same order as the self-induced Hall effect (which is caused by the electrons cutting the flux of their neighbours). Thus when it comes to charge distributions within plasmas, the relativistic electric field could be important.
But could these fields cause longitudinal stress in a metallic conductor, as has been suggested? Within the conductor we have:
![]()
where ![]() is the electric permittivity of vacuum, and r the radial
distance
from the center of the conductor. The maximum stress is at the
periphery,
where r = R. Observing that
is the electric permittivity of vacuum, and r the radial
distance
from the center of the conductor. The maximum stress is at the
periphery,
where r = R. Observing that ![]() and
and ![]() we get:
we get:
![]()
for the field at the periphery. The electric Maxwell stress is
![]()
where the left part of the expression on the righthand side is the same as the magnetic Maxwell stress we have studied earlier. As the drift velocity is very small, the Maxwell stress from the relativistic electric fields is negligible compared to the magnetic Maxwell stress.
It has been suggested that electric fields from surface charges may be of importance in some of the experiments with forces between parts of the same conductor [38]. The electric fields from surface charges in an electric circuit are essential for answering questions like:
Yet electric fields from surface charges are seldom mentioned in
textbooks,
causing a jump in the narrative between electrostatics and
magnetostatics![]() .
.
Let us consider a simple example, to see whether we have to count with these fields or not -- i.e. if they are strong enough to cause a substantial Maxwell stress, or if they can cause interaction forces between different parts of a circuit of a magnitude comparable to the magnetic forces. A circular circuit with a point dipole battery, see Figure 3.12, has been examined by Heald [32].
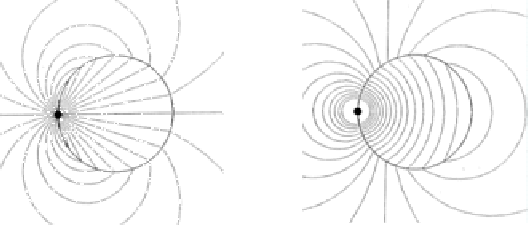
Figure 3.12: (A) Equi-potential lines (and also lines of energy
flux), (B) Electric field in the round circuit.
The battery is represented by the point, and the circuit by the darker circle. The magnitude of the electric field is:
![]()
where ![]() is the potential drop across the battery, and
is the potential drop across the battery, and ![]() the distance from origin (where the battery is). To sustain this field,
and thus the conduction, charges are set up on the surfaces of the
wire.
The radial component of this field can exceed the axial field (which
drives
the conduction) substantially, depending on the geometry of the
circuit.
Now, could this field cause a longitudinal Maxwell stress? The electric
Maxwell stress is given by:
the distance from origin (where the battery is). To sustain this field,
and thus the conduction, charges are set up on the surfaces of the
wire.
The radial component of this field can exceed the axial field (which
drives
the conduction) substantially, depending on the geometry of the
circuit.
Now, could this field cause a longitudinal Maxwell stress? The electric
Maxwell stress is given by:
![]()
Could this stress cause the breaks in Nasi ![]() owski's experiment? Typically for Nasi
owski's experiment? Typically for Nasi ![]() owski's experiment we have
owski's experiment we have ![]() ,
, ![]() (as the thin wire broke far from the battery). This gives,
(as the thin wire broke far from the battery). This gives,
![]()
which is negligible. Only very close to the battery, or where we have sharp bends, we could expect a higher stress.
Then what about forces between different parts of a circuit? According to Jefimenko, electric fields from surface charges can influence precision measurements of such forces [40]. A condition is that the capacity between different parts of a circuit is high compared to the inductance. In most of the experiments we have studied this has not been the case. Presence of materials with high electric permittivity (such as water) could enhance the forces substantially. Possibly, forces from surface charges could be of interest in the water-arc explosion experiments.
In this chapter we have analysed the Ampère electrodynamics and compared it with the Maxwell stress approach. We have seen how these are two sides of the same coin -- one focusing on charge carriers, and the other on the field properties. The forces predicted are of the same magnitude as the well known pinch forces, but act in other directions. As Graneau's `Finite current element analysis' mixes uniform and non-uniform stress, it over-estimates the stress, explaining why the longitudinal stress has been calculated to about ten times the stress from pinch forces.
The above approach could explain the phenomena observed in solid and liquid conductors. When it comes to dense plasmas, the forces are much stronger, and probably of different origin.
Relativistic electric fields may be important when it comes to the charge distribution in plasmas, but are far too weak to cause any longitudinal stress, nor any measurable forces between different parts of a metallic conductor.
Electric fields from surface charges may cause detectable forces in circuits with a large capacity to inductance ratio. However, that is not the case in the solid and liquid conductor experiments studied here.