Next: Theoretical discussion Up: Longitudinal electrodynamic forces Previous: Introduction
![]()
![]()
![]()
![]()
Next: Theoretical
discussion Up: Longitudinal
electrodynamic forces Previous: Introduction
In this chapter we discuss some (quite unnoticed) experiments in
which
longitudinal forces reveal themselves. As we shall see, several of the
experiments are open to different interpretations. The discussion
hopefully
sheds some light on where we could expect longitudinal forces in
experiments.
The presentation naturally has the character of a survey -- I refer to
the references for details![]() .
.
In 1961, Jan Nasi ![]() owski performed experiments with electrodynamic wire explosions [51,
52].
owski performed experiments with electrodynamic wire explosions [51,
52].
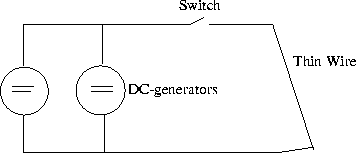
Figure 2.1: Nasi ![]() owski's circuit for the creation of wire fragments.
owski's circuit for the creation of wire fragments.
When subjected to a current pulse of sufficient magnitude a thin wire disintegrated into pieces in solid state, Figure 2.2.

Figure: Wire fragments created by a wire explosion. From Jan
Nasi
![]() owski,
Instytut Elektrotechniki, Warsaw, Poland.
owski,
Instytut Elektrotechniki, Warsaw, Poland.
When the segments were investigated it was found that the breaks
were
due tensile stress. Nasi ![]() owski found that a minimum current was needed to shatter the wire. By
using
wires of different diameters and materials, he derived that the tensile
force depended on the square of the current. However, the wires
shattered
after the current peak. Thus it wasn't until the conductor was severely
weakened by heating that the breaks could occur -- typically when the
wire
temperature had risen to 800-950°C.
owski found that a minimum current was needed to shatter the wire. By
using
wires of different diameters and materials, he derived that the tensile
force depended on the square of the current. However, the wires
shattered
after the current peak. Thus it wasn't until the conductor was severely
weakened by heating that the breaks could occur -- typically when the
wire
temperature had risen to 800-950°C.

Figure: Cracks due to stress in the wire. From Jan Nasi ![]() owski, Instytut Elektrotechniki, Warsaw, Poland.
owski, Instytut Elektrotechniki, Warsaw, Poland.
A section of a wire crack is shown in Figure 2.3. The dark band is molten metal created by the arcing in the gap.
Formerly it was believed that all wire disintegrations were due to
local
wire melting, as unduloids formed during overloading of a wire [4],
Figure 2.4.
Nasi ![]() owski showed that wire fragmentation could be caused independently of
the
unduloid formation.
owski showed that wire fragmentation could be caused independently of
the
unduloid formation.
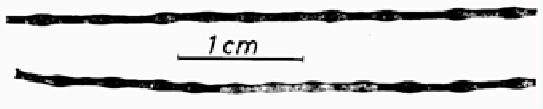
Figure: Unduloids formed by surface melting and pinch pressure.
From Jan Nasi ![]() owski, Instytut Elektrotechniki, Warsaw, Poland.
owski, Instytut Elektrotechniki, Warsaw, Poland.
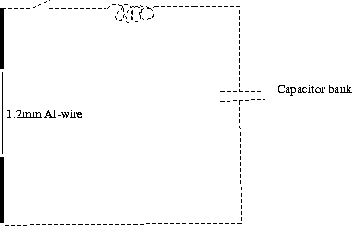
Figure 2.5: Graneau's experimental setup for wire fragmentation.
The experiments were repeated by Graneau with a slightly different setup, Figure 2.5. In order to avoid melting of the wire surface the DC-generators were substituted by a high voltage capacitor bank. Short high current pulses should be able to break the conductor before heat had been absorbed to such a degree as to melt the surface. This was exactly what Graneau found [17, 14, 16].
When the 1.2mm Al-wire was subjected to a short current pulse in the range 5-7kA, it broke into two pieces. With a higher current successive breaks occurred. Electron microscope investigation of the surfaces showed that the breaks were due to tensile stress.
Different explanations of the phenomenon have been proposed:
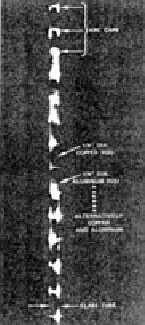
Figure: Separation and arc formation in the multi-arc generator.
From Peter Graneau, North-Eastern University, Boston, USA.
In Nasi ![]() owski's experiment a longitudinal stress, or repulsion, was observed in
the interior of a conductor. The question now arose if this repulsion
could
be observed more directly. This was studied by Ruscak and Bruce [62].
A 6.4mm copper rod was cut into 1cm pieces and stacked to 1m length in
a glass tube in vertical position. A light spring kept the pieces close
together. When current pulses of 3-30kA were discharged through the
column
the pieces separated and arcs formed in between them, Figure 2.6.
Some pieces spotwelded together by the arcs. Clearly, the rod pieces
seemed
to repel each other.
owski's experiment a longitudinal stress, or repulsion, was observed in
the interior of a conductor. The question now arose if this repulsion
could
be observed more directly. This was studied by Ruscak and Bruce [62].
A 6.4mm copper rod was cut into 1cm pieces and stacked to 1m length in
a glass tube in vertical position. A light spring kept the pieces close
together. When current pulses of 3-30kA were discharged through the
column
the pieces separated and arcs formed in between them, Figure 2.6.
Some pieces spotwelded together by the arcs. Clearly, the rod pieces
seemed
to repel each other.
Railguns were of interest in the 80s SDI-program. Today, interest in electromagnetic launching has revived in NASA's plans for a new kind of a space-shuttle. A railgun consists of two parallel bars and a transverse rod, the sleigh, Figure 2.7A. When a current is passed through the circuit the sleigh is accelerated due to the Lorentz forces (the conduction electrons in the sleigh move in the magnetic field from the bars). As can be seen, Figure 2.7B, these forces are strongest in the corner regions, and directed at right angles to the conductor, i.e. they are transverse. The recoil forces were expected to be seated in the rear, section III in Figure 2.7B. But recoil forces were also observed in the rails, the arrows in Figure 2.7A, pushing the rails back and thus deforming them. Some experimenters observed plastic deformation of the rails [5]. Others reported severe friction losses, which could be generated by transient bucking of the rails [21, 55].
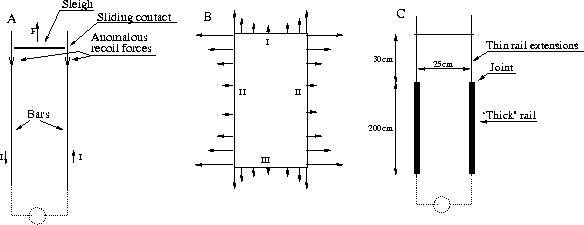
Figure 2.7: (A) Railgun principle. (B) Lorentz forces in the
rectangular
Railgun circuit. (C) Graneau's experimental setup.
Figure: (A) Inward deformation of aluminium rails. (B) Rails
before
deformation. (C) Bucking of steel rails. From Peter Graneau,
North-Eastern
University, Boston, USA.
Peter Graneau performed an experiment with thin rail extensions, Figure 2.7C, to demonstrate the seat of the recoil forces [21]. As the extensions were thin, they would easily be deformed if subjected to a backward push (like Euler breaking of a rod). The transverse sleigh was held fixed. When current pulses of up to 100kA were applied severe deformation of the rail extensions was observed. Figure 2.8 shows some of the deformed rails. Longitudinal recoil forces were obviously present in the rails (and rail extensions), deforming the parts that were unable to sustain the compression.
The possibility of actually weighing the repulsion between different parts of a circuit was first investigated by Cleveland [10]. Since then, many experiments have been performed to measure the force that one part of a conductor exerts on another part.
An experiment that often have been used in the debate is the impulse
pendulum![]() ,
invented by Pappas. It consists of a horizontally suspended rectangular
frame cut in two, where one of the halves is free to move. A current
pulse
imparts momentum on the moving pi-frame, which is carefully measured.
Precise
measurements have been made by Moyssides [50]
and Peoglos [54].
The total force seems to be correctly given by the Lorentz force.
However,
the Lorentz law does not account for the the fact that the intermediate
parts of the circuit are in a state of stress.
,
invented by Pappas. It consists of a horizontally suspended rectangular
frame cut in two, where one of the halves is free to move. A current
pulse
imparts momentum on the moving pi-frame, which is carefully measured.
Precise
measurements have been made by Moyssides [50]
and Peoglos [54].
The total force seems to be correctly given by the Lorentz force.
However,
the Lorentz law does not account for the the fact that the intermediate
parts of the circuit are in a state of stress.
Let us now study forces in liquid metal conductors. An abundance of experiments exists in this area, performed by Ampère [7], Neumann, Hering [35], Graneau [17] and others. Some of the most illuminating will be presented here.

Figure 2.9: One version of the hairpin experiment.
In this experiment, first performed by Ampère and de la Rive in 1822 [7], a bent metallic conductor is floating along two troughs filled with mercury when a current is passed through the circuit. The experiment was repeated by Tait, who substituted the hairpin with a mercury filled siphon [63]. This ruled out the possibility of thermal forces at the copper-mercury interfaces, which had been proposed as an alternative explanation. As mentioned above, Ampère's law would predict a force on the legs of the hairpin, whereas Grassmann's and Lorentz' would have all of the force seated in the transverse segment.
The hairpin experiment was repeated by Graneau [13], who noted that mercury was repelled from the rear faces of the hairpin. Ampère's law would explain this as a result of longitudinal repulsion, whereas field theory would interpret it as an effect of the diverging current in the mercury, just outside the face of the copper hairpin [36].
In order to investigate the mercury repulsion further, the following experiment was performed [17]:
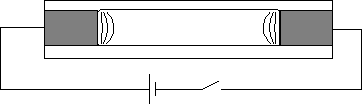
Figure 2.10: Agitation at the interface between solid and liquid
metal.
In a long rectangular mercury trough, with copper bars at its ends, a current of some hundred Ampère was passed. Wave patterns were observed near the the copper faces indicating a non-equilibrium in the conductor. Liquid metal seemed to flow away from the center of the copper face and then recirculate back at the periphery. The conductor thus seems to stretch itself at its center, like a compressed spring.
This is illustrated quite well in the liquid mercury fountain experiment in Figure 2.11:
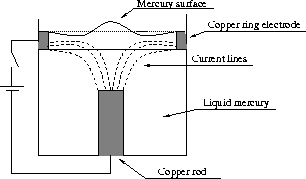
Figure 2.11: The liquid mercury fountain.
Metal flows away from the rod in the middle as it is being repelled, and the recirculates back. The jet from the rod causes the surface to rise in the middle of the cup [23].
One debated experiment is the copper submarine, invented by Northrup [53]. A pointed rod is floating in a mercury trough. When a current of approximately 400A is passed through the trough, the rod submerges and is propelled along the trough with the blunt end first, Figure 2.12. The submersion is due to the pinch forces (as `like currents attract').

Figure 2.12: The copper submarine.
The cause of the longitudinal motion is more debated. Northrup [53] attributed this to the hydrostatical pressure in the center, which is caused by the pinch forces. Hillas [36] has interpreted it as caused by the diverging currents at its ends. Graneau [13] suggested that the longitudinal repulsion predicted by Ampère's formula to be the cause of the movement.
The direction is the same if the current is reversed or if alternating current is used. This seems to be common for all these experiments, the forces varying with the square of the current.
In one of Hering's experiments a hooked wire is dipping into two mercury cups, one being narrow and the other one a wide dish,Figure 2.13. The wire moves decidedly to the right when a current is passed through. Hering explained this as being due to the stretching of the magnetic flux (the circles of magnetic flux around a conductor repelling each other). As the current is more concentrated in the narrow trough than in the wide dish (where the current diverges), the magnetic repulsion from the trough dominates, pushing the suspended wire to the right. The movement is independent of the direction of the current.
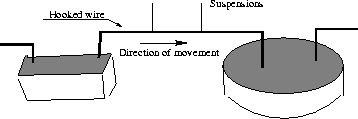
Figure 2.13: Wire movement between a narrow trough and a wide
dish.
In order to demonstrate that a conductor tends to stretch itself, Hering devised several experiments [35]. In one experiment a chain of copper was suspended in a mercury trough, Figure 2.14.
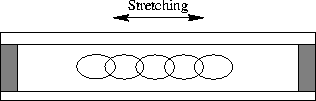
Figure 2.14: Stretching of a copper chain.
When current was passed through the circuit the chain stretched itself to its full length. Hering attributed this to the presence of more concentrated flux around the copper chain than around the mercury at its ends, the flux consequently trying to stretch the chain. He wrote:
`This experiment also meets the claims sometimes made that in some of the movements in these experiments it is the pinch effect which by its hydrodynamic action in the mercury causes the motion. If the pinch effect were to cause, it would act to push the ends of the chain towards the middle, but the fact is that the movement is in the opposite direction.'
A variant of this experiment was made by Graneau, where the chain was substituted by two copper bars, originally in contact, which separated under the action of the current, Figure 2.15. The repulsion between the bars was thus stronger than the repulsion between the copper-mercury interface.
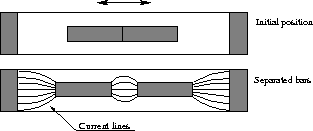
Figure 2.15: Repulsion between two copper rods originally in
contact
with each other.
In the previous sections we have studied forces in solids and liquid metals. Could the discussion be extended to dense plasmas, such as ionized water? As we shall see, new phenomena arise, making the situation a bit more complicated.
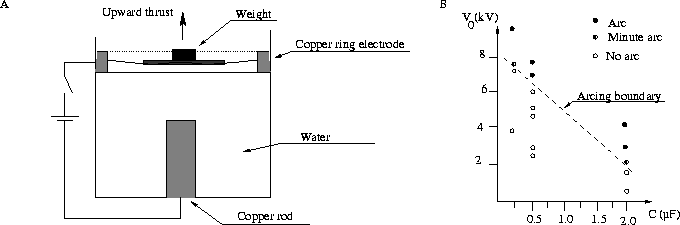
Figure 2.16: (A)The modified fountain experiment. (B) Explosion
threshold.
Peter and Neal Graneau carried out an experiment to look for longitudinal forces in water [18], Figure 2.16A. The mercury in the fountain experiment was replaced with water of varying salinity. Current pulses were discharged through the cup. In some cases the currents discharged silently, in others a luminous arc struck between the rod and the ring, accompanied by a hissing sound and shock waves in the water. The boundary between the two kinds of discharge depended on the total charge (Q) in the discharge, Figure 2.16B. This suggested that an arc formed when the number of ions present in the solution was insufficient to discharge the capacitor. The energy not dissipated through the electrolytic current obviously went into the arc discharge. With the same amount of energy, the discharge could either be silent or cause an arc explosion, depending on the combinations of the capacity and voltage of the capacitor.
In a typical experiment the average force during the explosion was 21.6N, throwing a 2.8g weight that was floating on the surface about 20cm up in the air, the current being about 94A. The calculated thrust from pinch forces was 0.55mN, too small to account for the force. Pinch thrust would also be present during the silent explosions, which proves that the observed force has something to do with the presence of an arc.
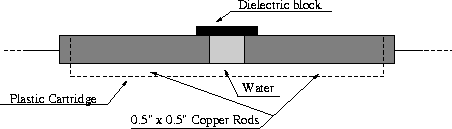
Figure 2.17: Experiment to create powerful water-plasma
explosions.
With another arrangement [19], Figure 2.17, current pulses in the range 10-25kA were used. The maximum force observed amounted to 430kN, equivalent to a pressure of 27'000 atm. If the water was free to move it would be expelled, emitting intense white light. When captured, it was found to be only lukewarm.
What is the cause of the explosions ?
If the excess energy turns out to be real this would be an interesting kind of `solar energy' (as it is the solar radiation that has to do the endothermic conversion from mist to steam), the Graneaus point out. Clearly, the phenomenon of water-arc explosions is still not well understood.
We have thus seen how solid conductors can bend and buckle, and even shatter, if subjected to high current pulses. The discussion indicates that some kind of longitudinal stress is present.
In liquid conductors the results are not as clear cut as with solids, as pinch forces play an important part. However, we can see how the idea that a current tends to stretch itself (in the middle especially) could be used to explain many of those experiments qualitatively.
It is clear that in some of the described experiments the forces could be regarded as a result of transverse pinch forces, at least intuitively. However, from an engineering point of view the concept of longitudinal stretching could be very useful, since it directs the thinking along other lines than the Lorentz equation does. This view is supported by the fact that modern textbooks seldom, if ever, mentions experiments like those we have discussed above. The creative value of the conceptual images in engineering should not be underestimated.
When it comes to dense plasmas the forces are magnitudes greater than what could be produced by pinch forces. Though still not well understood, the phenomena of electrodynamic water explosions may have many applications, as we shall see in Chapter 5.