Next: Experiments Up: Longitudinal electrodynamic forces Previous: Contents
![]()
![]()
![]()
![]()
Next: Experiments
Up: Longitudinal
electrodynamic forces Previous: Contents
During the last decade a discussion on longitudinal forces in conductors has been going on. The discussion is not new though -- it has recurred since the time of Ampère. In order to gain perspective a historical review is given in this chapter. In Chapter 2, I present some of the experiments connected with the phenomena. Various theories have been proposed to account for or disprove the existence of longitudinal forces. These are discussed in Chapter 3. Out of this discussion methods for calculation emerges, and the experiments are reexamined in the light of this in Chapter 4. The preceding discussion raises the question of possible applications of these phenomena. Some interesting applications such as metal punching, water-jet propulsion, high-current limiting and electrodynamic fusion are covered in Chapter 5. A novel application, the electrodynamic explosion motor, is also presented. The results are summarized in Chapter 6, followed by an extensive list of references.
The aim of this thesis is to awaken interest in the relatively unknown phenomenon of longitudinal forces in conductors. A survey of the area and some of its applications are given, together with a thorough theoretical discussion.
I would especially like to thank Dr. Peter Graneau and Dr. Jan Nasi
![]() owski,
for supplying me with articles and photos, and for answering my
many questions.
owski,
for supplying me with articles and photos, and for answering my
many questions.
The idea of longitudinal forces in electrodynamics (forces in the direction of current flow) dates back to the time of Ampère. In order to calculate the magnetic forces between two electric currents, Ampère subdivided each circuit into `current elements', Figure 1.1A and B. Through a series of ingenious experiments and some mathematical assumptions he arrived with a formula for the force between two such current elements. The total force on one of the circuits was then calculated by summing all the interactions between current elements in the different circuits.
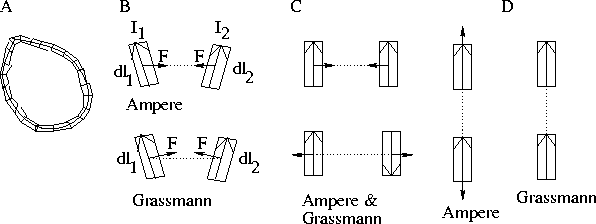
Figure 1.1: (A) Conductor subdivided into current elements. The
sum of the forces from the current elements in one circuit on those in
another gives the total magnetic force on that circuit. (B) Forces
between
current elements. (C) Transverse forces between parallel elements. (D)
Longitudinal forces between co-linear elements.
![]()
Here![]()
![]() is
the force the current element 1 (
is
the force the current element 1 ( ![]() ) exerts on current element 2 (
) exerts on current element 2 ( ![]() );
); ![]() and
and ![]() are the electric currents in the circuits;
are the electric currents in the circuits; ![]() is the magnetic permeability (a conversion factor);
is the magnetic permeability (a conversion factor); ![]() and
and ![]() are vectors in the directions of the current elements, see Figure 1.1B;
are vectors in the directions of the current elements, see Figure 1.1B;
![]() is the distance between the current elements; and
is the distance between the current elements; and ![]() the unit vector in the direction from
the unit vector in the direction from ![]() to
to ![]() .
.
This once famous formula, now almost forgotten in textbooks, predicted a longitudinal repulsion between two co-linear current elements, Figure 1.1D. To test the theory, Ampère and de la Rive performed an experiment in 1822, where a hairpin was to be propelled along two troughs of liquid mercury by the longitudinal repulsion [7]. It did so, and the experiment was considered a success for Ampère's theory.
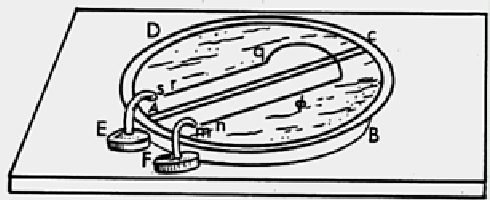
Figure: The hairpin experiment by Ampère and
de la Rive.
Longitudinal forces were not predicted by the force law derived by Grassmann.
![]()
His formula is sometimes incorrectly referred to as Ampère's
force law in modern textbooks [39].
It can be derived from Biot-Savart's law and the Lorentz force![]() .
According to Grassmann's law all the forces would reside in the
transverse
part of the hairpin, and thus only pull it from the front, rather than
also push the ends from behind, as predicted by Ampère. A
discussion
arose regarding which law was the correct one [65].
When integrated around a circuit they both yielded the same result, the
Neumann force law for two circuits [17,
9].
.
According to Grassmann's law all the forces would reside in the
transverse
part of the hairpin, and thus only pull it from the front, rather than
also push the ends from behind, as predicted by Ampère. A
discussion
arose regarding which law was the correct one [65].
When integrated around a circuit they both yielded the same result, the
Neumann force law for two circuits [17,
9].
![]()
But what about two parts of the same circuit? Ampère's followers advocated the hairpin experiment favored Ampère's law, but e.g. Maxwell argued that no matter what law was used the total force on the hairpin would be the same, as the laws were equal when a whole circuit was considered [43]. The possibility to measure exactly where in the circuit the forces resided was a question not pondered upon. Maxwell though remarked [44]:
`Of these four different assumptions [force laws] that of Ampère is undoubtedly the best, since it is the only one which makes the forces on the two elements not only equal and opposite but in the straight line which joins them.'
That is, only Ampère's formula obeys Newton's third law of equal action and reaction locally. The fact that Grassmann's (and thus Lorentz') doesn't was essential for the development of special relativity.
As the continental `action at a distance' theories gave way to Maxwell's field theory, Ampère's law was abandoned. Grassmann's law fitted in better with Maxwell's theory, as it was easy to relate his force to the magnetic field. Longitudinal forces were passed into the shadows for a while.

Figure 1.3: The pinch effect. (A) As `like currents attract',
the
conductor squeezes itself radially inward. If the material is too weak
to sustain the pressure it is pinched off at some point. (B) Pinch
depression
in a liquid conductor, caused by a current of some hundred Amperes.
The debate rekindled in 1921, initiated by Carl Hering who in 1907 had discovered the pinch effect in liquid conductors, Figure 1.3. He had also observed longitudinal forces but these had up to then been neglected by others.
In the 20s, confusion still reigned as to what laws of magnetic forces to be used. Engineers tended to rely on various laws of induction and reasonings like 'like currents attract, unlike repel', i.e. Neumann's law for two different circuits. Hering wrote several papers on the revision of these views, which spurred debate. His views on the matters were expressed clearly at the A.I.E.E. Midwinter convention in 1923:
`The strenuously opposed and long neglected longitudinal force was strongly upheld by some able discussers and disproved by none; the worst that the opponents could say about it was to the effect that they could get along without it.'
The fact that Maxwell's own field theory at least partially accounted for the longitudinal forces was clearly recognized by Hering. In Maxwell's theory a tension along the lines of magnetic and electric field existed, together with a pressure between the lines. Faraday had visualized lines of force and explained his discoveries in this geometrical language. Maxwell had cast Faraday's concepts into mathematical form and concluded that these stresses must exist in a medium -- the ether. From an hydrodynamical analogy he had then derived the existence of electromagnetic waves.
With special relativity the ether was abandoned -- although in a sense it wasn't, as Maxwell's stresses survived into Minkowski's energy-momentum-stress tensor. Minkowski's tensor was crucial for Einstein's development of general relativity [12], but is seldom covered to any extent in modern introductory textbooks -- they tend to discuss forces with the aid of the Lorentz equation.
In the 50s, Moon and Spencer derived a field free electrodynamics from Ampère's formula, as an alternative to field theory. They pointed out that induction and magnetic forces are by no means unambiguous from a student's point of view, if you go beyond textbook examples. They also noted that the debate around these paradoxes showed a certain pattern: `...interest seems to rise anew to a sharp peak, after which it gradually declines, leaving the subject much as it were before.' [48].
This was the state of affairs when Peter Graneau rediscovered some
of
Hering's experiments in the beginning of the 80s and begun a search for
longitudinal forces in literature and experiments [27].
He discovered the quite unknown papers by Jan Nasi ![]() owski, a Polish scientist who had discovered electrodynamic wire
fragmentation
in the 60s. A new debate begun, adding to the above-mentioned phenomena
anomalous railgun bucking, electrodynamic explosions in water and
several
other things.
owski, a Polish scientist who had discovered electrodynamic wire
fragmentation
in the 60s. A new debate begun, adding to the above-mentioned phenomena
anomalous railgun bucking, electrodynamic explosions in water and
several
other things.
Lars Johansson, Email: forename.surname@newphys.seSeptember 19:th 1996